Deep neural networks can produce highly accurate predictions. But if they have to make predictions far away from the training data (“out of distribution”), many network architectures yield catastrophically overconfident predictions. Ideally, the predictions for such out of distribution data should simply be “I don’t know”.
The Bayesian framework addresses this issue – it is named after the 18th century mathematician Thomas Bayes and provides a principled way to reason with uncertainty. It adds an a posteriori uncertainty to the network weights. Alas, in its exact form, Bayesian inference is often intractable. Even approximate Bayesian methods are often still impractical for large deep networks. They are not just expensive to run, but also hard to implement.
Laplace approximation as an easy-to-use option for uncertainty quantification
But a particularly simple form of approximate Bayesian deep learning is re-emerging as the fast, easy-to-use option for uncertainty quantification. It is becoming clearer that it does not just work well in practice, but also offers strong theoretical guarantees, as our recent paper has shown.
The Laplace approximation is a very old and simple idea. Deep learning algorithms find a weight vector that attains the highest point of an objective function (blue vertical line in Fig. 1). The Laplace approximation identifies uncertainty of this estimate with the curvature of the objective function around this point: A narrow peak corresponds to a confident weight estimate, wide peak corresponds to low confidence. This approximation is by no means perfect: it only captures a part of the true weight distribution. But in practice, it is often enough and provides surprisingly good performance for how simple it is. When used during predictions, this weight uncertainty then induces predictive uncertainty, as Fig. 1 illustrates.
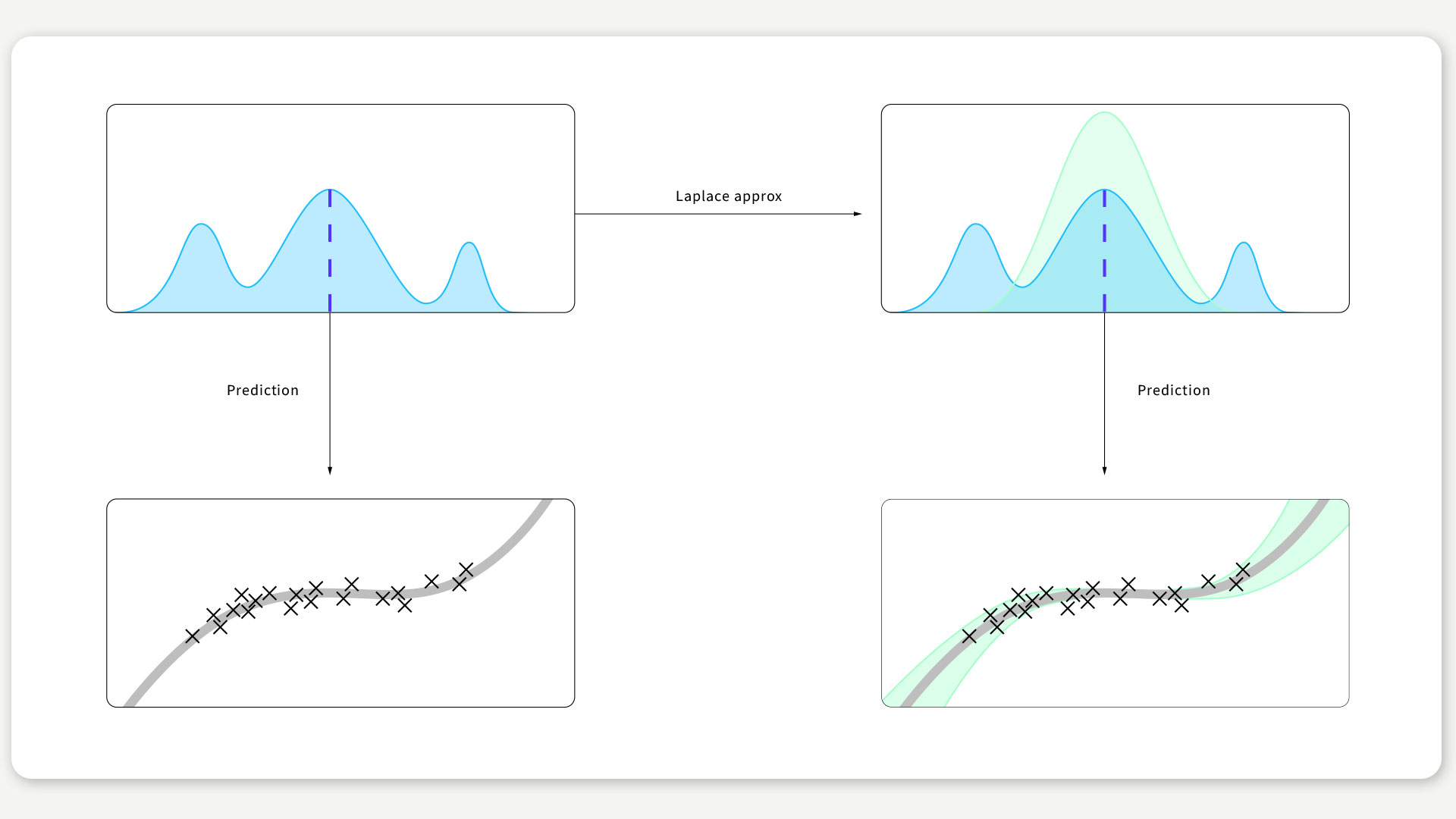
FIGURE 1 / Top: Light blue curve is the objective function. Dashed blue line is an estimate found by deep learning training. Green curve is the Laplace approximation. Bottom: Green shade is the error bar of the prediction (grey curve).
How to easily equip a DNN with uncertainty estimates
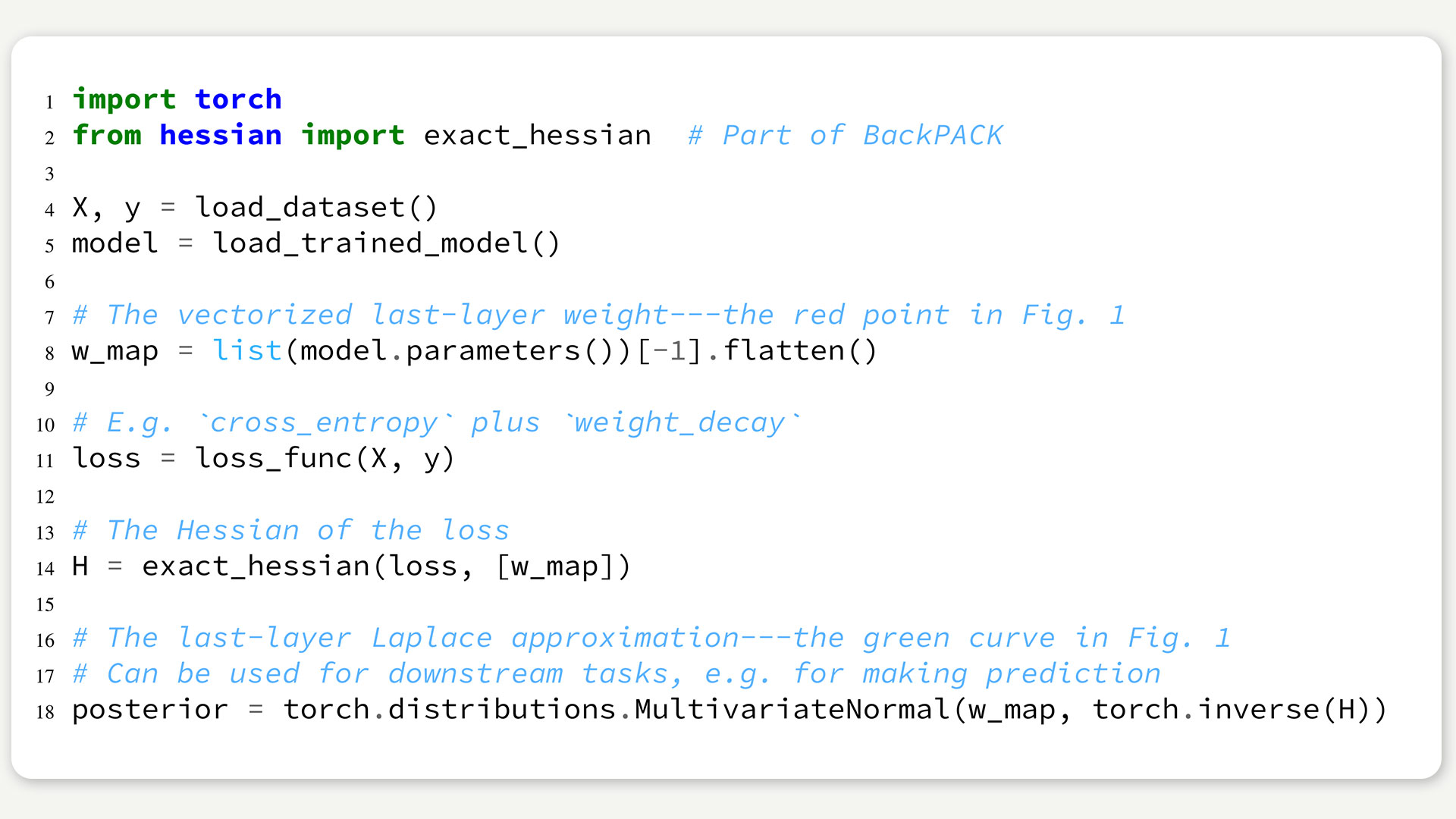
In our recent paper, we show that equipping a deep neural network with uncertainty estimates is about as simple as it gets: Train your network like usual, then consider only the last layer, and compute a manageably small matrix of second derivatives. Using modern tools like BackPACK (also developed in our lab), this can be achieved in just a few lines of extra code – example with PyTorch below. The result of this approach is now available in a software library, so there is easy access to uncertainty in deep neural networks for researchers and practitioners alike.
We emphasize that unlike other methods, this scheme can be applied on top of any pre-trained network, without hampering its accuracy. Moreover, for the popular case of deep neural networks with the ReLU activation function, we are also able to show that this approach prevents overconfidence on out of distribution data, see the figure below. Full code examples with step-by-step explanations are available here and here.
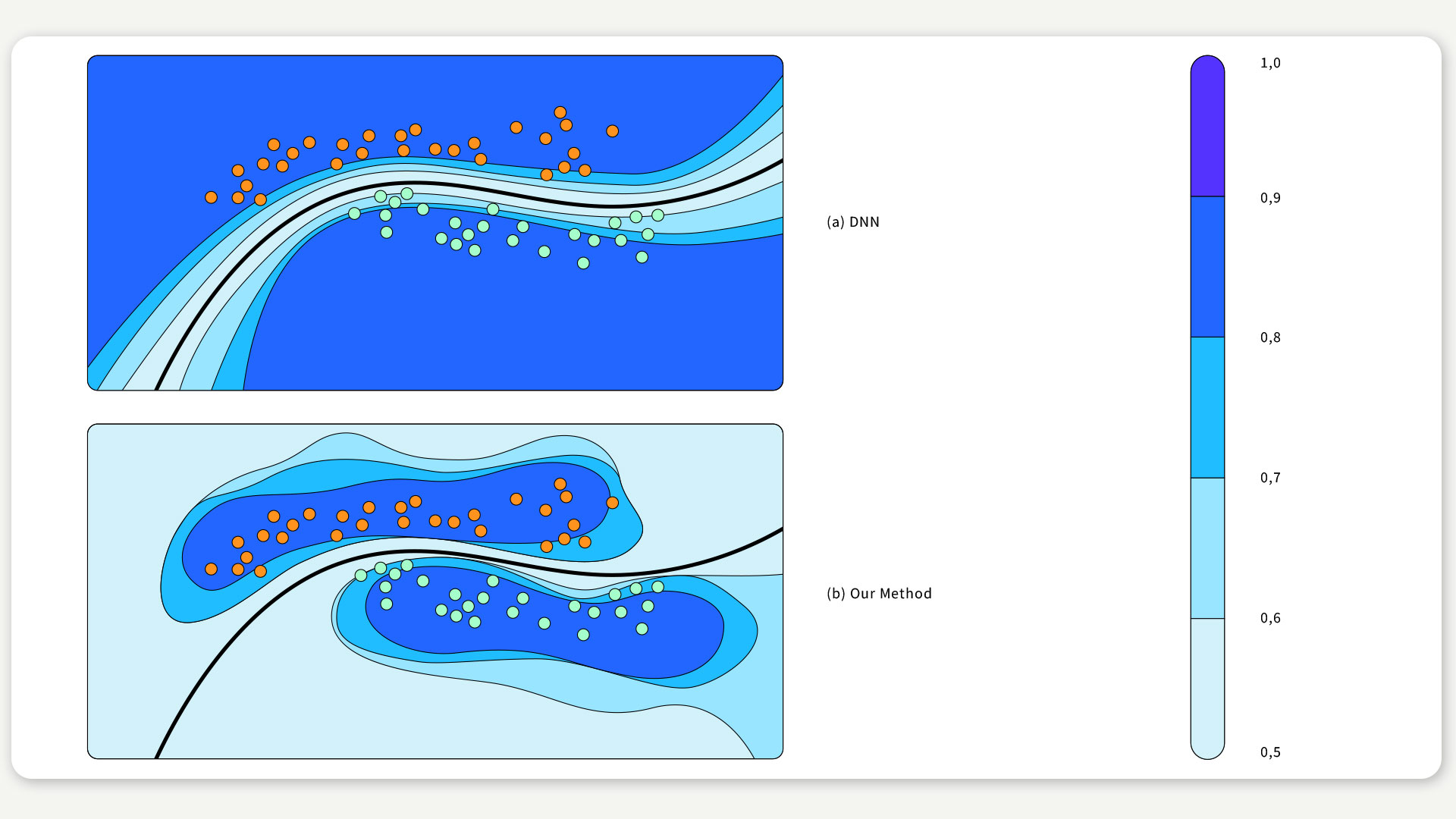
FIGURE 2 / Our method applied to a classification problem. Shade represents confidence estimate; black curve is decision boundary.
Text: Agustinus Kristiadi, Philipp Hennig
Cover illustration: Franz-Georg Stämmele
This text is based on the following papers:
[1] Felix Dangel, Frederik Kunstner, and Philipp Hennig. BackPACK: Packing more into Backprop. In ICLR, 2020.
[2] Matthias Hein, Maksym Andriushchenko, and Julian Bitterwolf. Why ReLU Networks Yield High-confidence Predictions Far Away from the Training Data and How to Mitigate the Problem. In CVPR, 2019.
[3] Geoffrey E Hinton and Drew Van Camp. Keeping the neural networks simple by minimizing the description length of the weights. In Proceedings of the sixth annual conference on Computational learning theory, pages 5–13. ACM, 1993.
[4] David JC MacKay. A practical bayesian framework for backpropagation networks. Neural computation, 4(3):448–472, 1992.
[5] Radford M Neal. Bayesian learning via stochastic dynamics. In Advances in neural information processing systems, pages 475–482, 1993.
[6] Anh Nguyen, Jason Yosinski, and Jeff Clune. Deep neural networks are easily fooled: High confidence predictions for unrecognizable images. In CVPR, 20157

Using Machine Learning for 3D Soil Mapping

Comments