Diffusion is an ubiquitous process in nature. Water diffuses in soil when we water our plants. Heat diffuses into a steak when we fry it. And chemical reactants diffuse through the test strip when we take a coronavirus self-test. However, applying diffusion equations from physics often requires simplifying assumptions to estimate unknown factors, such as diffusion rates. Such unknown factors can be learnt from data by physics-aware machine learning and first approaches have generated promising results. However, the mathematics behind current physics-aware machine learning models is mostly incomprehensible to scientists, which hinders knowledge discovery.
To illustrate the corresponding unknowns in a diffusion process, consider an accident that occurs in a factory. A large amount of chemicals is spilled on unsealed ground. How fast will the contamination penetrate, and how long will it persist in the soil, posing a risk to human health? The involved diffusion process is highly complex. Luckily, known rules from physics specify how substances diffuse in a medium. To apply these rules, though, certain substantial properties must be known, for example, how quickly the chemicals diffuse through the pore geometry of the soil. With our method, such properties can be precisely learned, such that it is finally possible to estimate accurately how the substance diffuses into the medium and how long it will persist.
FINN, a physics-aware neural network, completes the picture
With our approach, published at ICML 2022, we blend existing equations from physics and machine learning. In a collaborative effort among the research groups of Martin Butz (Cluster of Excellence “Machine Learning”, University of Tübingen, Germany) and Wolfgang Nowak (Cluster of Excellence SimTech, University of Stuttgart, Germany), Matthias Karlbauer and Timothy Praditia have developed FINN, which is short for FInite volume Neural Network. It is a physics-aware neural network model inspired by the so-called finite volume method from computational physics to solve diffusion equations; and the omnipresence of diffusion processes in nature implies a wide application of FINN.
Concretely, FINN builds on existing scientific equations as much as possible. To bridge the remaining gap between theory and data, we use machine learning – that is, we learn only those parts of the observations that we cannot yet explain with existing equations from physics. In order to later interpret these learned functions, it is important that the machine learning model structurally imitates the existing equations. To this end, FINN effectively mimics a physical equation where all unknown components are learned by dedicated modules (see figure 1). For example, dedicated neural network modules learn the velocity of the advection process, the retardation factor affecting the diffusion dynamics, or the reaction processes.
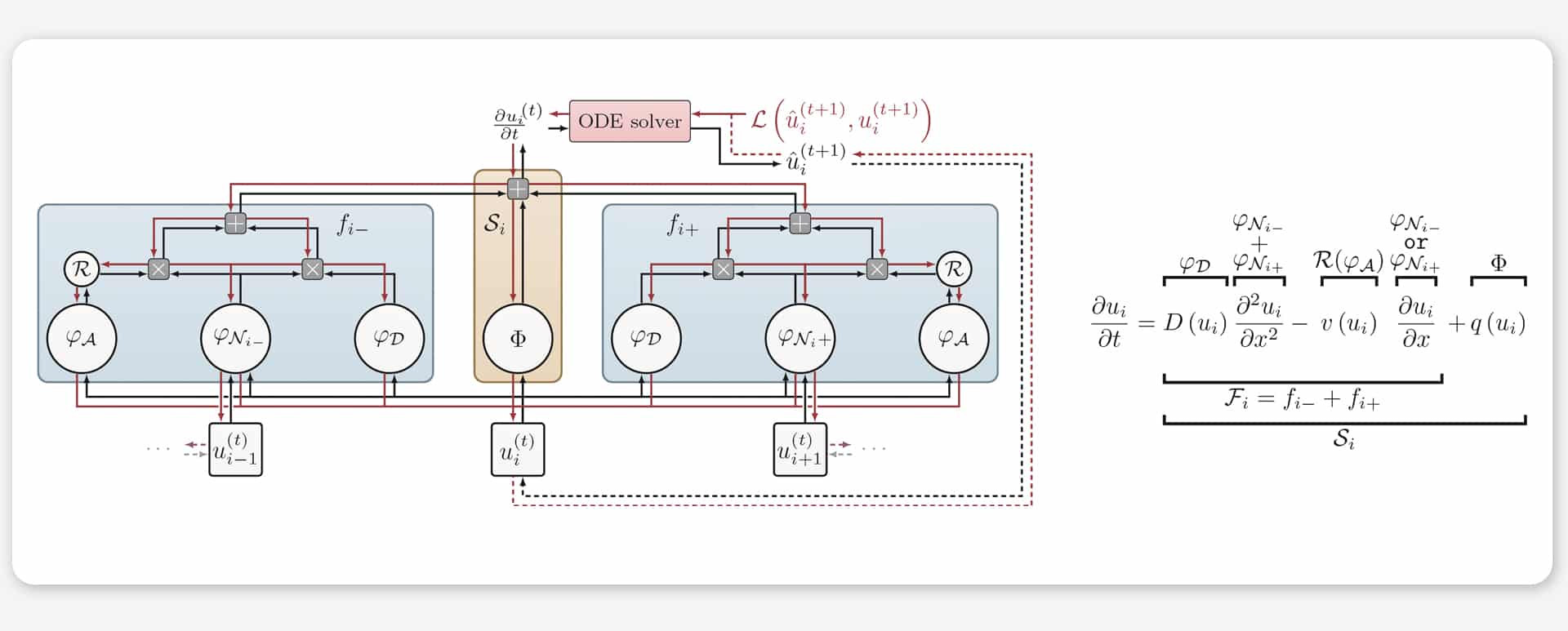
Figure 1: Left: Modularization scheme and information flow in FINN. The quantity of interest is depicted as u (e.g. coffee) and round circles correspond to trainable entities. Right: Advection-diffusion equation with different components, represented by FINN’s dedicated modules. Typically, some of these components are unknown, but can be learned by FINN.
The tricky part is that all these processes depend on the substance, the medium, and their interactions. Nevertheless, the modularization allows us to eventually nail down the exact physical function of all learned components and even to interpret them (compare figure 2). This is where previous methods fall short.
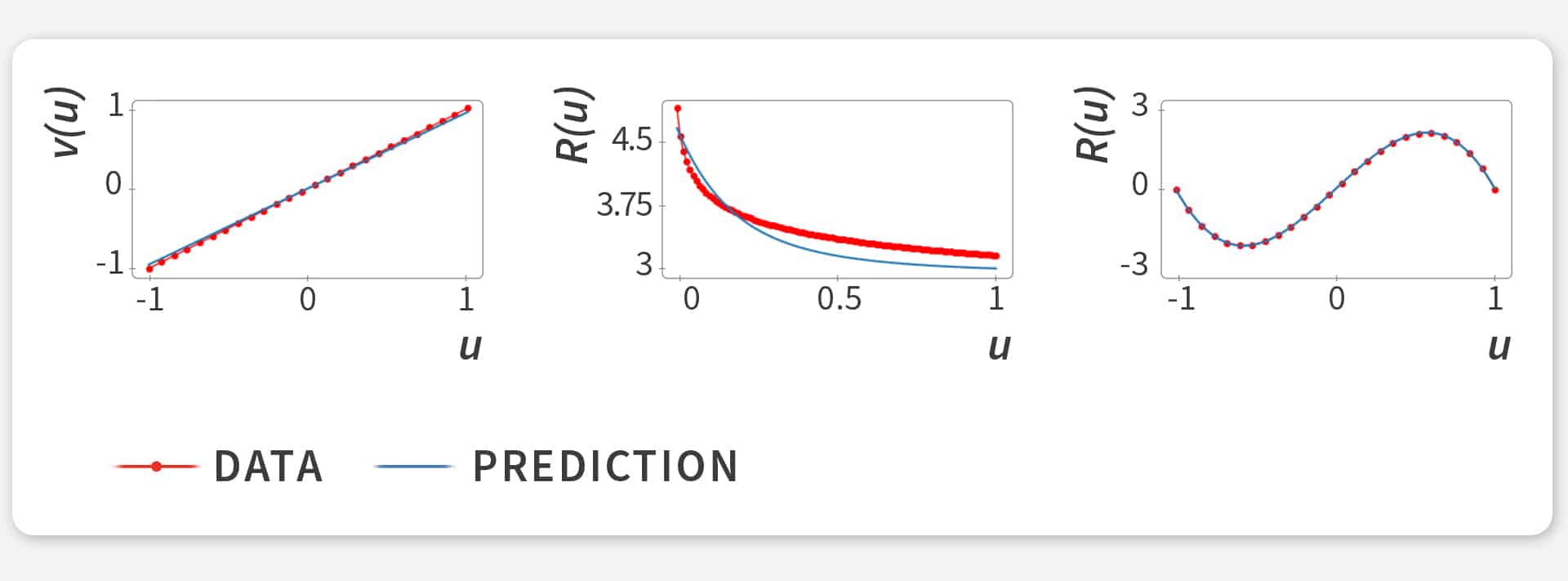
Figure 2: FINN was used to infer different kinds of unknown functions (blue lines) in three benchmarks. The data were generated synthetically and, accordingly, the true underlying functions were known (red lines with dots), but not provided to FINN. Left: velocity in the Burgers’ equation. Center and right: Retardation factors for the diffusion-sorption and Allen-Cahn equations.
Predicting the diffusion of contaminants in soils
We use our new model to study soil contamination in a small city in Canada called Kitchener. In this town, several cubic meters of trichloroethylene, a chemical abbreviated as TCE, were accidentally released on the premises of a company in the 1970s. TCE can cause cancer, DNA mutations, and affect unborn life. Yet, such chemicals were often used to remove grease during metal production as they dissolve fat easily and evaporate quickly. When spilled, TCE enters the soil and diffuses down through groundwater until it reaches an impermeable material – in this case a layer of clay several meters thick. Clay can absorb TCE over a very long period of time, but at the same time TCE will continue to slowly diffuse further into the surrounding environment and pose a substantial health risk to humans over several decades.
This is where FINN comes into play. We trained FINN to model the contamination processes in order to identify the soil’s unknown diffusion rate, without depending on prior assumptions (such as deciding on an isotherm function for sorption as required in traditional modeling). This allowed us to simulate the diffusion process for almost two months into the future, and to predict how it would behave under different initial and boundary conditions. This information can be used to provide more confident decision support in remediation planning and risk assessment.
Advancing Process Understanding in Diffusion Processes
Technically, our scheme can be applied to a broad range of physical processes, including heat and sound waves propagating in our planet’s atmosphere or fluid flow inside a pipe or underground. In essence, FINN can be used to characterize substance diffusion in any medium, raising the applicability of flow equations to a substantially higher level.
In a next step, we seek to employ FINN in weather prediction to describe particle motions through the atmosphere and explain processes that science has not yet uncovered.

Do machines see like humans? They are getting closer

Comments